As promised, moontower.ai includes a primer which is being dripped 1 post a week right here on substack.
Sign up to get early access here.
The moontower.ai Primer is divided into 2 units: Conceptual and Implementation.
To review, the Conceptual Unit which includes:
The Implementation Unit thus far:
Top of the Funnel: Cross-Sectional Fair Value
The top of the funnel is a set of cross-sectional tools to aid in assessing “fair value”. The top of the funnel consists of 4 tools:
Dashboard
Real Vol
Skew
Vol Scanner
Understanding Dashboard
Visit Dashboard
What is it?
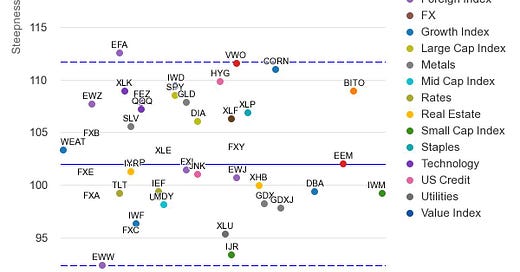
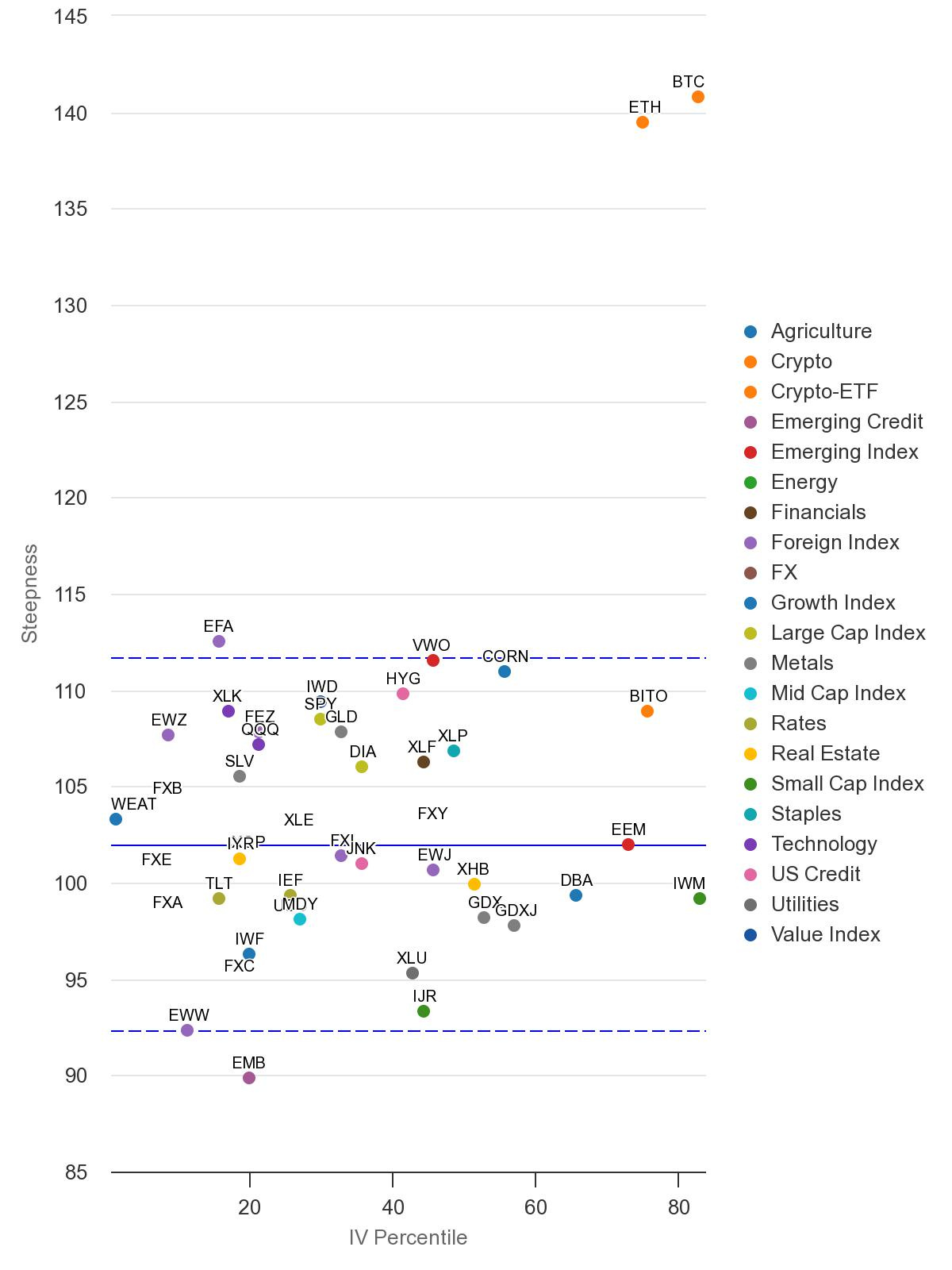
The Dashboard Chart provides a birds-eye view of the market. It’s a cross-sectional scatter plot across over 40+ assets, from equities to FX, commodities, and crypto.
The purpose of the Dashboard Chart is to give the trader a high-level overview of how the market is pricing implied volatility across the term structure and compared to its own history.
On the X axis, the chart plots the IV Percentile for every asset’s 1-month implied volatility. The IV percentile tells us the percentage of days over the last year when IV was lower than its present level.
On the Y axis, we show the Steepness metric. This calculates the steepness of the term structure for each asset, by taking the ratio of the 6-month IV vs. the 1-month IV. A steepness greater than 100 means the 6-month IV > 1-month IV, or an upward-sloping curve.
Interpretation
Many of the assets measured are highly liquid ETFs or reference highly liquid underlying markets. For example, TLT, an ETF that references the deep 20-year Treasury market is not only liquid, but more liquid than it appears because there are market-makers who focus on arbitraging the relationship between TLT, bond futures options, and the underlying bond options markets.
The volatility level and the term structure contextualize the supply and demand for volatility across time. The dotted lines represent a 1 standard deviation difference from the average steepness of the term structure.ApplyCtrl + EnterRemove
Since longer-dated IVs are less sensitive to recent underlying realized volatility they are partially anchored to longer-term expectations of volatility. Qualitatively, we can infer an element of mean-reversion baked into them. Empirically, we find that when near-dated vols become elevated the curve will “invert” as the near-dated volatility exceeds the longer-dated volatility. This means the near-dated volatility increased faster.
Similarly, when near-dated IVs are on the low to medium end we generally see an upward-sloping term structure.
Why is Dashboard the top of the funnel?
The dashboard sits at the top of the funnel because it is a quick and holistic way to see how the market is pricing volatility. If the points are clustered to the left, near the Y-axis, you can presume the market has not been stressed recently. IV is low compared to its 1-year history.
When you consider how large some of these markets are, you can presume the consensus pricing is driven by a tremendous amount of dollars. Like a Super Bowl line, you can expect the point spread to be difficult to beat. By seeing how the volatility “lines” are set we can infer that this is a reasonable gauge of fair volatility levels in the marketplace.
The dashboard also makes sense as an entry point because it focuses us on a reality that exists at the most zoomed-out level — there are only 4 categories of trades:
Buy long-dated vol
Buy short-dated vol
Sell long-dated vol
Sell short-dated vol
This a low-resolution statement. After all, a time spread or complex trade can take a leg in several of these categories but even then typically there is a “net” exposure that dominates one of these buckets. In addition, there are many ways to express these trades. The options you choose can vary by moneyness, they can be vertical spreads, and they can be sufficiently low delta that they don’t generate a meaningful vega.
Still, the simplification justifies the lack of nuance by allowing you to mentally understand what you are rooting for or how to narrow the type of trade you want to focus on based on your idea.
Is the volatility in XYZ cheap or expensive?
The Dashboard view of liquid volatility markets furnishes a sense of “fair”.
From this baseline, we can look for large aberrations in less liquid names, and think about whether they make sense or not. A less liquid name can be priced differently for several reasons:
1) Its recent behavior has diverged from its typical relationship to more liquid names.
2) It is pricing idiosyncratic elements that are not relevant to the liquid names.
Examples include:
known seasonality
an upcoming event, such as earnings or economic release
temporal flows that are out of sync with the general market ("vol has been declining in the overall market, but there’s persistent straddle buyer in XYX for the past week causing the IV to hold up relatively well")
Discretion and knowledge of the markets or flows can all be used to “adjust” for the differences. This is an irreducible aspect of trading. Any opportunity that arises from your measurement process comes with a disclaimer: “Is the divergence from what I expect justified?”
This is where the next set of tools lower down the funnel can be applied to a list of names that stuck out as “interesting”.
Understanding Real Vol
Visit Real Vol
What is it?
The Real Vol Chart is a cross-sectional view of implied versus realized volatility across assets.
The purpose of the chart is to quickly display if recent realized volatility is on the high or low end and compare this to the near-term IV.
The X-axis is the 1-year percentile of the trailing 1-month realized volatility. This will feel intuitive — “XYZ hasn’t been moving around too much lately, so I’m not surprised the realized volatility is in the 10th percentile”.
The Y-axis represents the volatility risk premium (VRP) computed as:
ln(1-month constant maturity implied volatility / 1-month realized volatility)
It is common for implied volatility to trade at a premium to realized volatility. The size of the premium is a proxy for how expensive the “carry” is on a long option.
Instead of computing a simple percent premium/discount to the realized volatility we use the natural log since the distribution of the ratio is closer to lognormal than normal — it is positively skewed.
The dotted lines represent 1 standard deviation differences from the average VRP of the sampled assets. Since lognormal statistics are normally distributed, the standard deviation measures maintain intuitive symmetry.
Interpretation
This chart earns its keep as a top-of-funnel tool because it rapidly sorts what’s typical from what’s potentially interesting, especially in conjunction with the Dashboard tool.
Implied volatility is a forward-looking measure reflecting the supply and demand for options. Consensus expectations of future realized volatility are embedded in the measure.
2 pronounced features of volatility are:
1) Clustering
Periods of high volatility or low volatility cluster, or have streaks. Not surprising. If volatility increases because of geopolitical headlines, it’s reasonable to expect volatility to remain elevated until there’s visibility of a resolution. A lack of visibility can persist.
Likewise, periods around holidays that have lower trading volumes can dampen volatility. Since holidays are known in advance, the market typically anticipates and discounts options prices.
2) Mean-reversion
Volatility doesn’t just trend towards infinite or zero forever unless the underlying asset ceases to exist.
Clustering and mean reversion are in constant tension.
Volatility can stay high or low for stretches of time before returning to “typical” levels, but it can also find a new typical. The volatility in natural gas markets derives from concerns of running out of storage on the downside during mild winters and having ample supplies on the upside during cold winters. The boom in shale supply during the 2010s shifted the volatility lower as the upside felt more bounded.
The Real Vol chart will tend towards a downward-sloping curve because of mean-reverting expectations.
At “low” volatilities, the VRP will expand as the IV will anticipate mean reversion to more typical volatility averages.
At "high" volatilities, the VRP will narrow as the market anticipates a decline in realized volatility.

VRP levels that are “off-the diagonal” anticipate clustering or persistence of unusual volatility levels. The chart can quickly bring your eye to such situations.
A note on known events
The VRP ratio divides IV, a forward-looking measure, by a lagging realized volatility. We understand both the embedded utility of such a measure —vol clusters, so recent volatility is correlated to the expected future volatility; and the tension that the numerator anticipates the future while the denominator reports the past. But there is a wrinkle around known events that distort our interpretation of the measure. The following examples characterize the distortion:
1) Upcoming earnings or FOMC day
Implied volatility will anticipate the extra variance associated with the upcoming event, artificially widening the VRP. Professional option traders will use quantitative methods to extract how much extra variance the market is assigning to the event to “clean” the IV. Ideally, VRPs would be adjusted for known events. There is no single accepted technique for cleaning the IV but the quick solution is a judgment — “XYZ has an abnormally high VRP, but I just noticed it has earnings next Tuesday”. [The moontower.ai roadmap includes providing a calculator to allow a user to extract an event. In the meantime, you can use term structure tools (described later) to “see” where the market anticipates events]
2) Earnings have recently been reported
This is the opposite failure mode of the VRP measure. A stock had a large earnings move which carries significant weight in the realized volatility (the denominator of VRP) but the IV is looking forward to a period where there is no news expected since the company has already given guidance, had a conference call, and reported financials. This will artificially depress the VRP. Again, judgment is in order. It’s best to compare the IV to periods of realized vol without the earnings move.
Understanding Skew
Visit Skew
What is it?
The Skew table is a cross-sectional view of implied skew.
It’s well understood that the supply and demand for options across delta or moneyness is not uniform. For the SPX index, investors tend to buy puts to hedge and sell calls to overwrite their core long equity positions. Out-of-the-money calls will tend to trade at a discount to the at-the-money volatility while downside puts trade at a premium volatility.
A common measure of the premium/discount to at-the-money volatility is called normalized skew.
Aside on computing normalized skew
It is a simple ratio of the volatility at an out-of-the-money point on the curve to the at-the-money volatility. It is common to measure at skew at the 25 and 10 delta strikes both on the upside and downside of the volatility surface and use the 50 delta option to normalize. (note the 50d strike is often but not always the at-the-money strike)
For example, assume:
Strike: 50 delta
IV: 28%
Strike: 25 delta put
IV: 32%
Normalized skew = OTM volatility/ ATM volatility - 1
Normalized skew = 32%/28% - 1 = 14.3%
The 25d put is trading at a 14% premium to the ATM volatility.
We call this normalized because the ratio is independent of the volatility level. Some measures of skew might take a simple difference. In this case, one could say that the 25d put is trading 4 vol points higher than the at-the-money which is true. But if we doubled the 50d IV to 64% and the put was still trading at a 4 vol point premium, normalized skew would compress to 6.25% premium of 50d IV. [68%/64% - 1 = 6.25%]
We use normalized skew to be able to compare the relative cheapness or expansiveness of the skew over time regardless of the at-the-money IV level.
The Skew Table has 2 primary views.
1) Normalized skew levels
The table displays 25 delta and 10 delta skew levels (both on the upside strikes or “call side”, and downside strikes or “put side”) for the asset universe.
Mods:
The user selects the maturity
The columns are sortable
2) Normalized skew percentiles
Toggling to the percentile view allows the user to see the percentile the skew measure occupies (1-year window) for a given maturity. The term 'maturity' refers to the nearest maturity to the specified term. The percentile view allows users to compare the skew with the typical skew associated with a fixed time to expiration.
Interpretation
The Skew table allows a user to quickly scan for names where the skew is low or high.
Consider an approach that starts with an axe to buy cheap downside protection:
Filter for the maturity of interest
Find names with normalized put skew in a low percentile.
If you already had it in mind that you’d like to buy options in XYZ but were agnostic about the strike you could look at the skew to see if an out-of-the-money is relatively more attractive than the at-the-money strike range.
Understanding Vol Scanner
Visit Vol Scanner
How does it work?
1) The maturities are at set intervals:
3d, 7d, 14d, 30d, 60d, 90d, 180d, 365d
The tool selects the closest maturity listed for each asset using option chain data. This choice is a compromise between displaying each asset's unique maturities whether or not they are shared with other assets. It provides a bird’s eye view in a digestible, standard format. The user can drilldown into a particular asset’s vol scanner on the Tickers tool.
2) The change shown is the percent change in the volatility for the user-chosen delta.
A percent change in the volatility means if implied volatility increased from 20% to 21% that is a 5% change (as opposed to a 1% change in the level of volatility also known as a “click” change). We choose percent change to make comparisons between vol changes across assets. If a 100 vol name and a 50 vol name both have a 1 vol point click change we want to recognize that this is more significant for the 50 vol name.
Aside on "percent vega"
This might seem foreign to traders who measure volatility risk with raw vega numbers. For example, if you are long 1,000 vega and volatility increases by a point from 20 to 21, you expect to make $1,000.
To make your p/l scale to percent changes simply multiply your vega by the volatility itself. So 1000 vega x 20% volatility = 200 “percent vega”. If volatility increases by 5% from 20 to 21, your p/l scales with percent vega —> 5 x 200 = $1,000!
Percent vega has the advantage of allowing you to group vega risk across assets regardless of volatility level. It does not make it strictly superior but it is common for traders to measure volatility risk in many ways depending on the context.
You don’t need to convert your risk software’s vega into percent vega. Remember the vol scanner is a tool to view how volatility has changed today and percent changes allow us to normalize the comparisons.
3) The normalize toggle
Percent changes calculations allow us to compare volatility changes across assets. Normalize allows us to compare volatility changes across the term structure (in a later discussion of volatility cones you will see that long-dated implied volatility fluctuates less than near-dated volatility). If a 3-month IV changes from 20 to 21 this is less significant than a 12-month IV changing from 20 to 21.
Why?
Because the 12-month option has 2x the amount of vega as the 3-month option. So the p/l will be 2x as large for the same change in volatility.
Another way to say this is if both IV’s increase by 1 point, the value of the calendar spread will increase. If the 12-month volatility increased by only 1/2 a point the calendar spread would have stayed the same value.
If a term structure was perfectly flat (every month has the same IV) option prices would vary in proportion to sqrt(ratio of time). So a 12-month option at 20% volatility is worth 2x a 3-month option at 20% volatility because sqrt(12/3) = 2
This property allows us to scale volatility changes easily.
The user can fix a fulcrum or the “normalize factor” to 90 days, for example. We can then multiply all the volatility changes by sqrt(time to expiry/90).
Example:
The 90-day IV increased from 20 to 21. A 5% change. Let’s scale the change by the “normalize factor” of 90:
5% x sqrt(90/90) = 5%
Let’s say the 180-day IV also increased from 20 to 21, a raw percent change of 5%. Let’s scale that change by the “normalize factor”:
5% x sqrt(180/90) = 7.07%
This makes sense… a 5% change in a 180-day IV is more significant than a 5% change in a 90-day IV. The scaled changes of 5% and 7.07% reflect that. And in fact, the calendar spread will have increased in value! Remember, your p/l depends on changes in option premium (ie calendar spreads). Volatility changes are proxies for premium changes and this adjustment is a better indicator of how the premiums changed than simply looking at raw IV changes.
4) If you choose not to normalize the changes in IV select OFF.
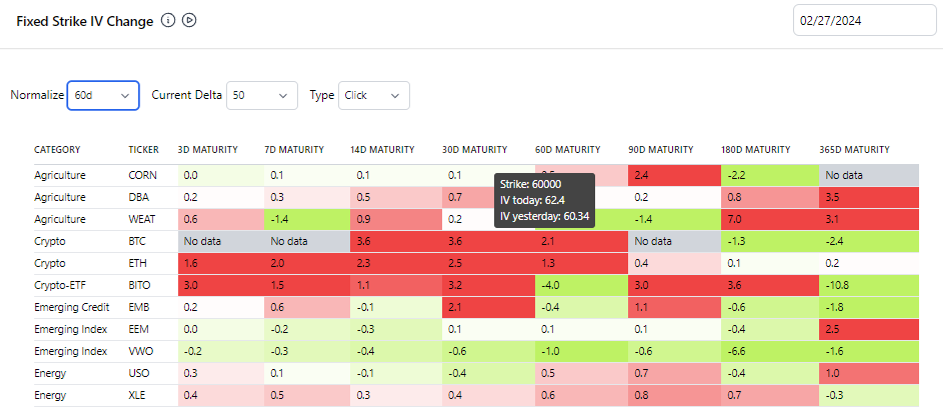
The vol scanner is a useful execution/timing tool. Once your analysis has narrowed down options you may want to buy or sell, vol scanner let’s you see how they are performing on a relative basis.
For example, if the options you want to sell are outperforming the other vols cross-sectionally it may be a good time to place offers in the market. On a vol desk, the scanner is useful for deciding where to set “electronic eyes” or track down voice brokers who might be buying those options pushing up their vols. It’s a way to sell into buyers to minimize slippage or even have an edge.
References
Extra: Using Scaled Vega to Summarize Risk
Suppose you sum your vega risk across the term structure to report a net raw vega.
The net vega will do a poor job predicting how much profit or loss to incur on a change in volatility. If I said the 90d IV increased by 1 point and your net vega is 1000 then you might expect to make $1,000 profit.
But what if your raw vega was the sum of the following:
+4000 in the 365-day bucket
-3000 vega in the 90d bucket
If IV increased by 1 point in the 90d volatility I would expect to lose $3,000 in that bucket.
But my best guess of how volatility changed in the 365-day bucket might be such that calendar spread stayed the same — which means I expect volatility only increased by sqrt(90/365) or .5.
.5 x +4000 vega = $2,000
On balance, if you say “90d IV increased by 1 point”, I’d actually expect that I lost $1,000!
[Because +$2000 - $3000 = -$1,000]
If I had normalized all my vega exposures to the 90d using sqrt(90/time to expiry) I could compute a scaled vega:
My net scaled vega would show that I was actually short 1,000 vega scaled to 90d.
When volatility increases by 1 point, I’m not surprised that my p/l is -$1,000!