one-touch

Moontower #264

Mar 23, 2025

Friends,

I’m in Vegas this weekend to celebrate a friend’s 50th. Between March Madness, Dead & Co returning to the Sphere and the ETF Exchange conference, it’s a zoo.

I went on the website for the conference. Lots of familiar faces amongst speakers. Yinh and I will grab a coffee with

kyla scanlon

today if we can steal a moment.

Fun fact, but Kyla is the single largest referrer to this substack with more than 4k subs driven. I’ve known her since she had me talk to the On Deck Investing cohort back in 2021. She used to write about options long ago! I started following that first blog of hers which must feel like a lifetime ago given her rise.

This is from her interview with Tyler Cowen:

I’m such a fan of seeing such a sharp, upright mind successfully find traction in the influencer/journalistic/author world. The incentives there always threaten to corrupt or get lead to audience-capture but she has navigated the minefield with a rare combination of maturity, groundedness, and honesty.

It’s funny, I can’t imagine thinking about options at 16 years old. But those stories exist. If I recall, Jeff Yass started noticing arbitrages in the option prices published in the newspaper as early as 12 or 13. He said something about liking TV dinners, so he looked up the company Swanson to buy calls on it. Munger said that Buffet also had a very strong grasp of options by the time he was a teen and understood the theory intuitively.

The subtitle of this substack is a clickbait riff on the whole moontower theme:

“a stoner dad explains options trading to his kids”

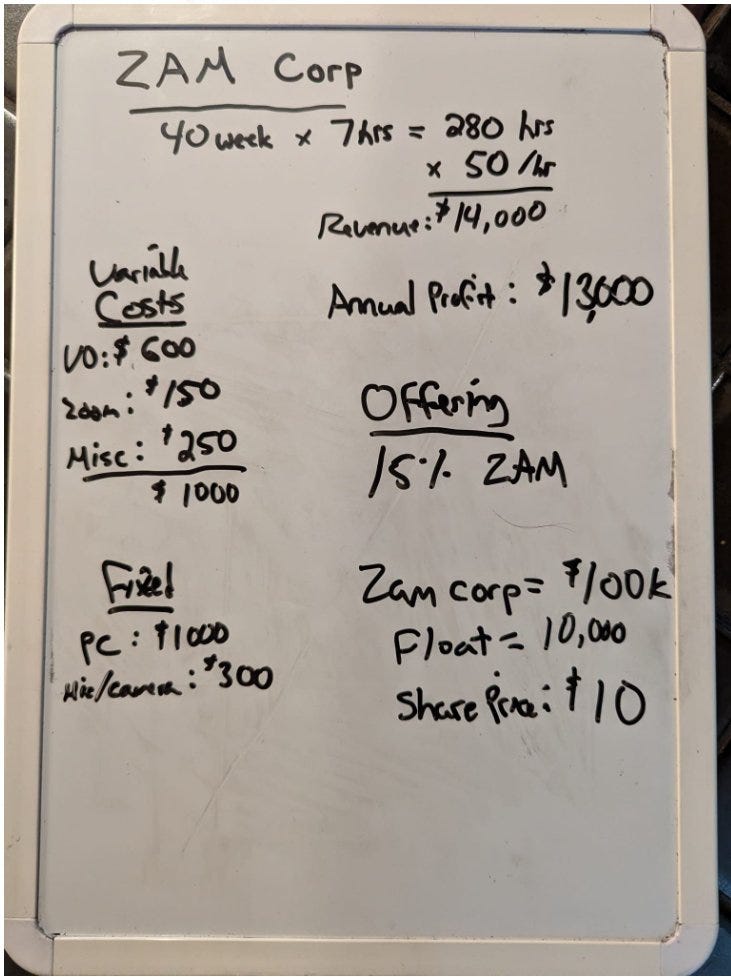
But this past weekend I really did start teaching the 11-year-old options. We refreshed the idea of what a stock is.

His imaginary company teaches kids to “vibe code” (these are some games he’s made. He hosts them on a page he made in Github and to be completely forthright, I don’t really understand what he did nor did I know he had a Git account).

I started by explaining calls and puts, moneyness, and what an option is worth at expiration.

His 1st homework:

This is the curriculum for the foreseeable future:

hockey stick diagrams
minimum and maximum arbitrage bounds
hockey stick diagrams with stock positions
Put-Call Parity
Synthetic stock
What makes options worth more (time and volatility — he grasped this immediately just in conversation which impressed me but we’ll tighten it up so that’ll mean a foray into standard deviation. Which shouldn’t be tough, he just did mean absolute deviation in Math Academy which I learned is a seventh-grade topic. I mean it when I say all the math we do here is high school at best!)

My goal is after some options ed he vibe-codes a timed put-call parity game which our devs can then wire into moontower.ai.

I told him I want him to be able to work with me for money and he seems to like the idea but I’m not clenching too hard. Even work that is fun can be a chore so you need to cross a certain motivational threshold to sustain through when it’s a drag. There’s a fragile period from where one sits today and crossing that threshold so I find it’s best to tread lightly until you see the renewable glimmer.

[This has happened with Math Academy. I had to push at first although not even that much but as he got into it, I’m more likely to tell him to chill out on the lessons and come play video games with me because he got to the point of self-motivation. But this is a big change from prior years where I had to nudge more. Even though, I never pushed that hard bc of my own childhood PTSD.]

Anyway, I’ll report back on how this experiment develops.

Money Angle

Elm Wealth published an article on a ubiquitous personal finance topic:

How Much Insurance is Right For You? (8 min read)
James White & Victor Haghani

It covers:

Insurance sizing framework
Alas, free lunches are hard to find
We should be sensitive to margin, rather than premium
Risks come in all sizes
The Campbell-Ramadorai (CR) rule of thumb
Small risks
Bundling of big and small risks
Moral hazard
Other insurable risks
Financial market insurance

From the conclusion (emphasis mine):

The insurance decision is primarily a function of the size of the hazard relative to a family’s total wealth, the family’s risk-aversion, and the margin in the insurance policy being considered. Families can readily figure out the first two inputs to their decision, but they are ill-equipped to determine the degree of margin. We hope that this note increases awareness of the central role of margin in the insurance decision

The impact of the margin felt intuitively large. Which is a flipside I suppose of why Buffet is so rich -)

Money Angle For Masochists

2 weeks ago I shared this tweet:

By saying I’d buy that proposition I’m saying “I’d buy that vol”

Andy, responded with a joke about what’s the “one touch” option worth, which I asked him to delete because I really would have liked a fool to sell me that proposition and Andy’s comment gives away the sauce.

[X’s killer app would be to escrow bets, but that’s another convo altogether]

I’d be a size buyer of a 50% probability that we get back to the highs before the end of the year.

It’s not bullishness. It’s vol trading. If you could buy that probability for 50% you could arb it vs the value of a one-touch call that pays off “if the stock ever touches or exceeds the strike price before expiry’.

That call will trade for a higher implied probability than 50%.

I’ve alluded to the rule of thumb before, but a one-touch probability is approximately twice the delta. At the time Andy tweeted, the highs would have corresponded to the 10% out-of-the-money call strike.

If we double the delta of that call, we estimate the one touch probability. Given SPX vol, I knew immediately that a 10% OTM call expiring on Dec 31 has a higher delta than 25% so the one-touch probability would certainly be at least 50% bid.

So as a matter of education there’s multiple lessons in this simple exchange.

Estimating the one-touch probability

Using our rule of thumb, we just need to estimate the delta.

@quantian’s got that trader reflex — do the napkin math:

What did he do in steps:

Used VIX as a proxy for implied vol which is annualized
Scaled it to 9 months using √time or √.75… 25% * √.75 ~21.7%
10% / 21.7% ~ .46 sigma
1- normdist(.46) ~ .35 probability [assumes probability ~ delta]
Double the probability —> 70% chance of one-touch

😈Possible enhancements to the estimate if you are a masochist:

With VIX at 25 I’d expect the term structure to be inverted so 9 month vol is lower. This would lead you to be more conservative on your delta. Sigma is directly proportional to our vol estimate so if we use 75% of the vol our sigma increases by 1/3 (since we dropped lowered the vol by 1/4). Normdist is not a linear function so still use the calculator and that pushes the delta down to .27 or 54% probability.
The delta depends on the the moneyness of the forward price not the spot price and since interest is greater than dividends for SPY the delta is a touch higher.
We’ll assume the positive skew embedded in Black-Scholes lognormality assumption offsets negative call skew. In sum I’d sell quantian’s delta of .35 and buy a delta of .27 so let’s call the fair delta .31 and the probability of the one-touch as 62%. I love getting even money odds when I should be laying 5-3.

Someone else knows their options btw:

My response to quantian showed another way to conservatively estimate that the probability was higher than 50%

Intuition for why one-touch probability is 2x the probability of expiring ITM

I’ve discussed the shortcut before in crossing over zero. But I sketched an intuitive example using a trader’s favorite binkie — the binomial tree.

The image is self-contained explanation and follows from a simple assumption of a stock 50/50 to go up or down $1.

Starting from $100 and traveling 5 periods what’s the probability of the stock expiring $99 vs the probability of it “touching” less than $99?

Learn more:

Estimating the probability of a stock expiring above or below a strike from the delta works for relatively low vol or short dated option. The below post explains the real meaning of delta and why/how that estimate can break down:

Lessons from the .50 delta option

Trader Math

I’ve included the one-touch probability in the wiki-style collection:

Math Shortcuts Traders Know By Heart

Videos this week

Stay Groovy

☮️

Moontower Weekly Recap

Refer a friend

Need help analyzing a business, investment or career decision?

Book a call with me.

It's $500 for 60 minutes. Let's work through your problem together. If you're not satisfied, you get a refund.

Let me know what you want to discuss and I’ll give you a straight answer on whether I can be helpful before we chat.

I started doing these in early 2022 by accident via inbound inquiries from readers. So I hung out a shingle through the Substack Meetings beta. You can see how I’ve helped others:

📲Book A Meeting