Mission Plan #4: Vega & Theta Mission: Capture VRP (including covered calls/puts)

Mission Plan Series #4

Jun 10, 2024

moontower.ai has released a new series —> The Moontower Mission Plan

This guides a step-by-step progression for developing opinions on volatility which you can use whether you are trading options to bet on volatility itself, or more likely, to bet on direction.

An installment will be released once a week right here on substack.

If you want to access the entire Plan now, you can become a free member here.

The idea that options are structurally overpriced invites many investors and traders to sell them to capture the volatility risk premium (VRP).

The retail perspective

Sophisticated retail traders like many of you understand the concept of a risk premium.

It’s like a form of “beta”.

Equity Risk Premium as Compensation

Consider the SP500. There’s an equity risk premium. See Index Investing: The Nature of the Proposition. The premium is a fair compensation for patience and tolerating drawdowns. But it’s not compensation for labor. Even a toddler can hit a “buy” button on SPY.

Volatility Risk Premium as Compensation

You can glance at the moontower Dashboard on any day to see evidence of a volatility risk premium. We can import the same equity risk premium logic to the VRP:

Passive attempts to capture VRPs should yield results commensurate with the risk. The option seller is being paid to underwrite non-linear, skewed insurance-like liability.

Retail traders range from sophisticated to not-yet-sophisticated. (There are also the “hopeless” but there’s no chance those folks are drawn to the moontower). If you currently sell options to capture the VRP there is a good chance you are doing so in a directional way — by selling covered calls or cash secured puts.

If you do this without any analysis you should expect over a large sample size to collect an average amount of VRP.

💡The problem with “Average VRP”

The average VRP is an extremely low-resolution concept.

Why?

1. The cross-sectional lens in Dashboard looks beyond the “averages” and shows that under the hood there are names that are relatively cheap and expensive compared to some baseline premium. Without such a lens, you might be selling vol that looks cheap on a relative or possibly absolute basis.
2. VRPs can vary over time. There are periods where the asset management world falls in love with option-selling overwhelming the amount of capital willing to own or delta-hedge long optionality.

So the concept of “average” VRP is neither constant over time nor within a cross-sectional snapshot.

Adopting a professional perspective

Additional compensation for work

If there’s no labor in your vol-selling process, I would not expect the risk-adjusted returns to levitate above rough concepts of an efficient frontier.

Research, risk management, process, and execution are all required if you want to earn more than beta. This is labor. Of course this is not plumbing or dentistry. Labor is a necessary but insufficient condition for excess returns. Returns are noisy — cavities are not.

But the reason you are here is moontower is a tool for doing work so you can do better than your passive implementations.

Let’s state the basics

1) Theta is not an edge. It’s just the cost of gamma. It can be too expensive or too cheap.

If a $100 stock has a 10% chance of going to $200 then selling the 150-strike call for $1 isn’t income. You have sold something worth $5 (10% chance the option is worth $50) for 80% below its actuarial value. The option has a theta, but not as much as it should if it was priced properly.

2) If you sell an option for a higher implied vol than what the asset realizes, on average you will win. But it’s a messy, path dependent process.

If you sold that $150 strike call for $6 you still lose 10% of the time even if the long-run expectancy is positive.

The lifecycle of a short vol trade

By now you understand that this is not a house-flipping seminar where we clap and cheer when we hear the words “passive income”.

The directional vol seller

The most gentle on-ramp to selling options are covered calls and cash-secured puts for positions where you either own the stock or interested in buying it if it falls. Unlike the naive option-selling approach, you follow the process in Formulating An Axe List to see if the names are strong candidates for selling vol.

We expect this to be the most common approach for moontower users interested in selling vol. You are trading around your own directional axe.

The agnostic vol seller

A smaller number of users will formulate an axe list without any directional bias. They will use the funnel to filter for option selling opportunities, strain the opportunities through a final discretion/context filter, and proceed with the trade.

The primary difference in approaches is the agnostic starts with a blank slate whereas the standard investor will check their directional axes against the vol funnel to see if there’s an option-selling opportunity on their short list of names.

Both approaches occur in stages.

Identify the target & structure
Size the trade
Execute the trade
Manage the position
Exit

I’m going to briefly step through the stages. I say briefly because volumes can be written about this.

📖Book rec

Moontower user and friend Euan Sinclair has written the best books about practical option management. His books have been the light for many traders. Positional Options Trading is his most recent volume. It’s a slim read but packed with useful insight. I published notes but they are no substitute for the original.

Step 1: Identify the target and structure

We identified targets in Formulating The Axe List as well as the structure for trades with directional bias.

What about structuring for agnostic vol sellers?

Because the agnostic seller has no opinion on direction, they will initiate the trade “delta neutral”.

The most popular examples of these trades is selling straddles or strangles.

A more constrained way to sell vol delta neutral is to sell:

a) iron condors: simultaneously selling an OTM call spread and OTM put spread. Another way to say the same thing — you sell a strangle and buy a further OTM strangle for less premium to cap your risk

b) iron butterflies: selling a straddle and buying a strangle to cap your risk

Step 2: Sizing

Again there are books written on sizing, so I’ll simply offer what I do:

I work backwards from how much risk I’m willing to take.

To do this it’s important to note the 2 largest drivers of your p/l:

a) Vega

b) Gamma

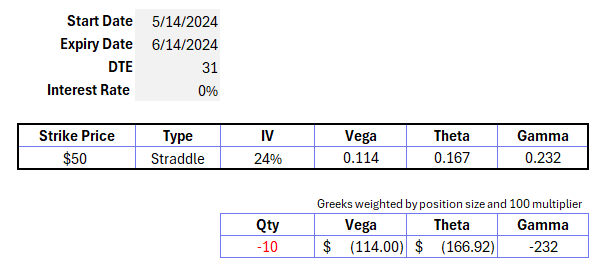
Suppose I sell 10 1-month straddles at 24% vol in a $50 stock. My option greeks:

Greeks per straddle and cumulative for 10 straddle position

Because you sold the ATM straddle, your initial delta is 0.

What do the rest of these position-weighted greeks mean?

Vega: If IV increases (decreases) you lose (earn) $114

Theta: You earn $167 per day

Gamma: If the stock moves up (down) you get short (long) 232 deltas. You can think of a delta as a share.

Because you are short gamma, when the stock goes up, you get shorter and vice versa.

Scenario: Small move

What’s our expected p/l if IV is unchanged and the stock goes up 1% or $.50?

First note, at 24% volatility the implied daily volatility is 24%/√251 or 1.5%. The stock only moved 1%. This should be a winning day for being short a straddle.

Let’s attribute p/l to each greek:

Delta: $0 —> You’re starting delta is 0 so there’s no p/l attributable to delta

Vega: $0 —> IV on the strike you are short did not change

Theta: +$167 —> The options erode

Gamma: We only moved $.50 so our delta only gets shorter by half the gamma. By the time the stock lands at $50.50 we are short 116 deltas instead of 232. We started at 0 delta and end -116 deltas. We can estimate that we were then short 58 deltas on average for over a $.50 move. Therefore our estimated p/l due to gamma is -58 * $.50 = -$29

If you are short options, gamma p/l is always negative since you get shorter on rallies and longer on sell-offs.

Sum of the P/L from the greeks = $0 + $0 + $167 - $29 = $138

The realized move was smaller than what was implied by the straddle so we win!

Scenario: Large move

What’s our expected p/l if IV is unchanged and the stock goes up 4% or $2?

Delta: $0 —> You’re starting delta is 0 so there’s no p/l attributable to delta

Vega: $0 —> IV on the strike you are short didn’t change

Theta: +$167 —> The options erode

Gamma: We rallied $2 so our delta gets shorter by 2x the gamma because gamma is defined as per $1 move. By the time the stock lands at $52 we are short 464 deltas. We started at 0 delta and end -464 deltas. We can estimate that we were then short 232 deltas on average over a $2 move. Therefore our estimated p/l due to gamma is -232 * $2 = -$464

Sum of the P/L from the greeks = $0 + $0 + $167 - $464 = -$297

A 4% daily move is larger than what was implied by 24% vol, so we expect this is a bad day.

💡Greeks change!

Greeks are snapshots. Like an option itself, the value change with moneyness, volatility, time, and interest rates/divs. When we attribute P/L to greeks it is approximate.

In the above example, the theta of the straddle is $167 when it’s exactly ATM, but once the stock moves the theta will be smaller as the strike is “further” away. $167 will be an overestimate. This is true for gamma as well.

Also note -- we assumed vega was unchanged. But in the first scenario, vol may decline on such a small move and vice versa for the large move scenario. Therefore, your vega and gamma p/l’s are correlated amplifying both winning and losing days. This is a very broad rule with many exceptions.

Contextualizing the risk

The 50-strike straddle at 24% vol with a month until expiry is worth $2.74.

If you sell 10 straddles you collect 10 x 100 multiplier x $2.74 = $2,740

If you sold the straddle at 24% vol because you believe the fair vol is 20% you expect to make 4 vol points of edge over the life of the trade.

4 vol points x $114 of vega = $456 over the life of the trade.

Let’s compare that to the risk.

In our small and large move scenarios we saw that your daily p/l can easily vary by $200 with a month until expiry.

But as time elapses, the theta and gamma per option will increase if you remain near the strike (of course this means you are probably winning nicely on the trade) as the option premium shrinks. Your p/l variance will grow.

Let’s re-evaluate greeks with 5 days until expiry.

The straddle is worth $1.05

Greeks:

The theta and gamma have almost tripled with the stock sitting on the strike with 5 days to go.

Now it’s reasonable to expect your p/l standard deviation has tripled to something like $600 per day.

But again, if the stock has moved away from the strike, your greeks will dwindle muting the p/l swings of a delta neutral position.

💡More on those changing greeks...

You might note how the vega of the option shrinks giving the illusion that IV risk is lower. This is counterbalanced by the IV itself becoming more volatile as time passes. The net result is vega p/l sensitivity remains fairly consistent over the life of the option.

Like the other greeks, if the stock moves away from the strike, the vega also falls

This surfaces a key point:

If you expect to make 4 vol points on these 10 straddles and the standard deviation of realized vol itself is say 10 points it’s a .40 Sharpe trade. But the experience of this trade is that if you end up being short lots of gamma the Sharpe will be lower because your p/l swings will be high. But you are also happy to be short a straddle and find that over the course of a month the stock hasn’t strayed far from the strike!

All of this points to needing a visceral feel for option risk. It is something that come from practice. Trade small as you learn. If you are uncomfortable you are too big.

This is my simple prescription:

For typical stock and vol moves (say less than 2 standard deviations), the greeks are a great guide to p/l fluctuations
For large moves, use a shock framework

Scenarios shocks work better for estimating p/l over large moves. Greeks are useful for "local" changes.

Each cell is a scenario = p/l of the repriced option + delta p/l from any share position at start of day

[Note: If you are hedging the delta to get back to neutral every day you will have a share position against your option position.]

Step 3: Execute the trade

Revisit Thoughts On Execution, Greeks, and Weights from the Primer

If your broker allows you to construct multi-leg trades as a package that save you from needing to leg the desired option structure invitng the possibility of getting “hung” on a spread (for example you want to buy a call spread and you lead by purchasing the near leg, get filled, and watch as vol collapses as you try to sell the higher strike.)

Step 4: Manage the trade

You opened the trade agnostic on direction. You are simply trying to capture the vol. You can balance your delta back to neutral by trading the stock daily, weekly, multiple times per day.

The tradeoff:

The more frequently you hedge, the lower the overall p/l volatility. The cost of this reduced risk is transaction + slippage costs

If you hedge too infrequently, the p/l due to delta risk is likely to swamp any vol edge you have.

💡An alternative to delta hedging frequently (pros only)

Having a large sample of trades on that diversify each other. Market makers do this by letting offsetting beta-weighted deltas cancel each other and simply hedging the residual with SP500 minis. They will still constrain how much gross exposure they have to any single name because of idiosyncratic risk.

Step 5: Exit

You identified the trade in the first place by running it through the funnel outlined in Formulating An Axe List. Once you have a position, you should continue to check it against vol axes as markets change.

If a vol you thought was expensive is now cheap you should cover it regardless of whether you made or lost money. The outlook for the trade is indifferent to your p/l. All that matters is “cheap or expensive now?”

There is tremendous noise associated with trading. Especially in options. While we always prefer to maintain a discretionary filter to our trades, that is not cover to be obstinate about our positions whenever it suits. If you go against a vol axe, or press one after it has dissolved the burden of proof is on your reasoning.

References