idios everywhere
Moontower Munchies #75
Friends,
We shipped 2 more calculators to moontower.ai. They are free, shareable and embeddable.
Options Hedge Ratios Calculator
The hedge ratios calculator computes how many dollars of asset B you need to hedge asset A.
Hedge ratios can be useful for long/short pairs, hedging a basket or single stock with an index future, or translating option deltas from one name to another.
A hedge ratio multiples the beta between the 2 assets by the dollar amounts. The main inputs are the volatilities of each asset (implied or realized depending on user preference) and a correlation.
In the example, you are hedging a $1mm long notional position in a 40% vol name. The annual standard deviation of P/L is $400k.
If ES (ie e-mini SP500) is 80% correlated and 15% vol you’d need about $2.1mm worth of futures (about 8 contracts at current SPX level) to hedge. That would cut your portfolio standard deviation almost in half. You’d still have $240k “risk remaining”.
“Risk remaining” is how we referred to this quantity however today it’s more commonly referred to as “idio” for “idiosynctatic risk”. It’s the risk not explained by the broader benchmark.
In practice, this was a useful calculation because you always face a tradeoff between reducing risk and the cost to hedge. If I’m trading gold and in the course of market-making I take on some long deltas, but I have some short deltas in silver, then I can quickly check “Is my risk remaining in gold terms tolerable?” Fine, don’t hedge.
It’s true that correlations and vols themselves are volatile, so running large delta spreads for long periods that rest on their stability is not advised. But neither is hedging all the time. These calcs give you the numerical context to guide the hedging decision.
More details on the computation can be found in From CAPM To Hedging: How CAPM can help us compute hedge ratios and estimate "idio" risk.
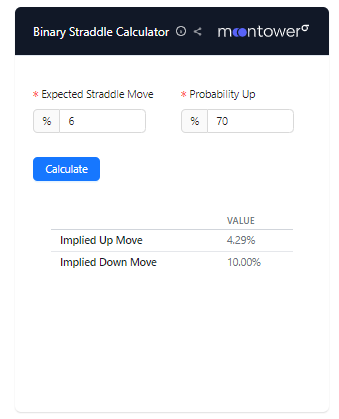
If you believe an upcoming move reduces to 2 possible outcomes (FDA ruling, merger arb, election) and can estimate the probability of up vs. down, then the straddle price implies how much the asset is expected to move in either of the 2 directions.
This calculator computes the expected move sizes for a binary event given a straddle price and the probability of an up or down move. It will become more handy as prediction markets grow,in turn, making implied binary probabilities more legible.
[In last week’s The Grammar of Trading, Todd Simkin mentioned that SIG is now a market-maker on the CFTC-regulated Kalshi exchange where you can bet on event outcomes.
This is news from earlier this month:
Interactive Brokers Launches Forecast Contracts on Economic and Climate Indicators]
For a detailed example of the calculator’s computation see Binary Straddle Example Based On The 2016 Election
A new learning project
This is the preamble to a large new post that I’ll be releasing in part or in whole (haven’t decided yet) in tomorrow’s Moontower issue:
An Introduction to Dynamically Hedged Option Positions
Active traders and investors buy and sell bonds, stocks, and commodities because they have a view that the asset is cheap or expensive. Sometimes they will use options to express their bets. They are experts in discerning value in these “underlying” securities.
Derivative traders who make up a tiny overall portion of the investing landscape are not experts in the underlying, but instead, they are focused on pricing the securities that “derive” their value from the price behavior of the underlying. Futures, forwards, ETFs, and options are common examples of derivative securities.
The derivatives trader doesn’t hold a high conviction view on the direction of the underlying. Instead, the trader pencils out how much it would cost to “replicate” the payoffs of the derivative in various states of the world using a mix of cash (and interest) + the underlying securities. This entire framework is referred to as arbitrage pricing.
Arbitrage pricing, unlike other pricing frameworks such as CAPM (capital asset pricing model) starts with The Law of One Price. This law is not like a law that comes from Congress. It’s the idea that identical future payoffs should have the same cost today regardless of the portfolio that generated them. It is the basis of option pricing theory.
Why options are a special type of derivative
Option pricing theory asserts that an active trading strategy in the shares of an asset XYZ can replicate the payoff to an option on XYZ if we know:
the expiry date of the option
the strike price
the current price of XYZ which determines the option’s moneyness or distance from the strike
the interest and dividends from now until expiry
the volatility or size of X’s price fluctuations
Our confidence in these inputs varies.
Extremely confident
The strike and expiry are the only inputs we are 100% certain of.
Highly Confident
We can infer interest rates from the yield curve. If the stock becomes hard to borrow, we have less confidence in the proper discount rate.
We can estimate dividends based on past behavior and company guidance.
In normal market conditions, we are highly confident in these inputs. Still, our error bars can widen dramatically during market-wide stress or if there is idiosyncratic news in XYZ we are trading.
We can estimate the current price by looking at the stock’s bid/ask spread.
Medium to extremely low confidence
We have extremely low confidence in the price of XYZ over the life of the option.
We have low confidence in the magnitude of future moves in XYZ. The disagreements about what the volatility can be give rise to a very specific form of derivatives trader:
The Volatility Trader
The volatility trader, like other derivatives traders (such as so-called Delta One traders), doesn’t make a living based on views on the underlying. Volatility traders have opinions about, well, the volatility. This means a view of how the asset moves, how the option surface changes, and ultimately what it costs to replicate various options or spread options against each other to “leg” into attractive propositions based on an understanding of arbitrage bounds.
While the price of an option is sensitive to all the inputs mentioned above, the volatility trader typically only holds a differentiated opinion on the volatility. When the trader buys or sells the option they are inheriting a sensitivity to drivers they have no opinion about. By analogy, the pharma investor who buys a drug company is exposed to the economy at large, a system that they don’t have a refined view of. The pharma investor may “hedge” out extraneous exposures as best they can since they want to live and die by their drug company analysis, not the wider ripples of national enterprise.
Similarly, the volatility trader wants to sterilize the impact of the non-volatility inputs.
Those other non-volatility inputs tend to be stable over the life of the option — except for the stock price itself which affects the option’s moneyness. The option trader wants to hedge against “directional” moves in the stock. They don’t care if the stock goes up or down, they only care about how the magnitude of the moves compares to the magnitude implied in the option price.
Dynamic Hedging
The volatility trader sterilizes the sensitivity of the option to direction by “delta hedging”. They want to be delta-neutral just as a long-short stock picker tries to stay “market-neutral”. The analogy is strong. A market-neutral trader is out of balance as soon as the stocks in their portfolio start moving, the “delta-neutral” volatility trader is out of balance as soon as the stock ticks and the option moneyness changes.
A major assumption in the Black-Scholes model is that you can continuously hedge the delta. Unfortunately, nobody told the real-world to comply. It is prohibitively expensive to hedge the delta every minute or second, to say nothing of doing so on infinitely small time slices.
Option traders compromise their desire to “isolate the vol” by staying delta-neutral with the cost of frequent hedging. Said otherwise, the cost of this noise introduced to their p/l is less than the direct costs of minimizing directional risk.
So what do volatility traders do in practice?
They hedge at discrete intervals. This is called “dynamic hedging”.
So what schedule do they hedge on?
Well, you might as well have asked how many religions exist. It’s a giant topic. Taleb even published a book called Dynamic Hedging.
While there are many ways to craft a hedging schedule the key is the tradeoff at the core of the problem:
We want to isolate our source of edge…but hedging unwanted exposure is always a cost.
Our tolerance for risk is weighed against the size of our edge and how often we get to take at-bats.
🔗See If You Make Money Every Day, You’re Not Maximizing (A Treatise on Hedging)
Tune in tomorrow to see where this is heading…til then
Stay Groovy
☮️
Need help analyzing a business, investment or career decision?
Book a call with me.
It's $500 for 60 minutes. Let's work through your problem together. If you're not satisfied, you get a refund.
Let me know what you want to discuss and I’ll give you a straight answer on whether I can be helpful before we chat.
I started doing these in early 2022 by accident via inbound inquiries from readers. So I hung out a shingle through the Substack Meetings beta. You can see how I’ve helped others:
Moontower On The Web
📡All Moontower Meta Blog Posts
👤About Me
Specific Moontower Projects
🧀MoontowerMoney
👽MoontowerQuant
🌟Affirmations and North Stars
🧠Moontower Brain-Plug In
Curations
✒️Moontower’s Favorite Posts By Others
🔖Guides To Reading I Enjoyed
🛋️Investment Blogs I Read
📚Book Ideas for Kids
Fun
🎙️Moontower Music
🍸Moontower Cocktails
🎲Moontower Boardgaming



i've used these equations millions of times but the way you write about them makes me think about them in a different way and spurs so many ideas. It seems like you go back and reason through them again and in doing so uncover different framings of them which unlocks creativity.
Thanks for all the good work!